28 juin 2007
4
28
/06
/juin
/2007
22:08
La différence entre masse inerte et masse pesante m’apparaît d’une grande subtilité, j’en suis fasciné tout autant que par la démarche du physicien hongrois Roland Eötvös (1848 – 1919), qui passe trente années de sa vie (à partir de 1886) à caractériser expérimentalement cette différence. Ses travaux sont d’autant plus fondamentaux qu’ils inspirent Einstein en 1907 dans son principe d’équivalence entre gravitation (masse pesante) et accélération (masse inerte), prélude à la relativité générale de 1916 ; encore aujourd’hui, les physiciens vérifient dans l’espace en permanence la relativité générale, notamment en mesurant au plus précis l’identité entre masse inerte et masse pesante.La masse inerte mi intervient dans le principe fondamental de la dynamique f=miγ ou dans la quantité de mouvement p= miv ; la masse pesante ou masse grave mg intervient dans la force de gravitation ou d’attraction de Newton f= G´ mg´ M/R², où M et R sont la masse et le rayon terrestres. Votre masse inerte est celle qui va vers l’avant quand le métro freine brusquement, votre masse pesante est celle de votre poids sur la balance.
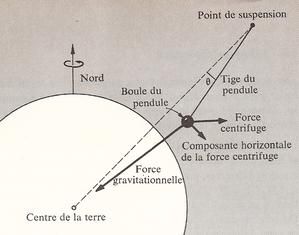L’association la plus parlante entre ces deux masses est celle du pendule, ou tout simplement du fil à plomb. La force centrifuge liée à la rotation de la Terre sur elle-même influe sur le fil à plomb suivant sa latitude : au pôle, elle est nulle, et le fil à plomb est dirigé vers le centre de la terre ; à l’équateur, elle n’est pas nulle, mais dans la même direction que le poids, en sens contraire, le fil indique donc le centre de la Terre ; en une latitude autre, la force centrifuge (et la masse pesante) dévie légèrement la direction du fil à plomb par rapport au centre de la Terre… Pour donner quelques formules, la composante radiale du poids est mgg, sa composante horizontale dûe à l’inertie centrifuge terrestre est mi Ω² R sinλ cosλ, λ étant la latitude et Ω la vitesse de rotation de la Terre . L’angle de déviation par rapport à la radiale terrestre est très faible, égal à Ω² R sinλ cosλ /g, soit 1,7 x 10-3 x sin(2 λ). Quand λ= 0 ou 90°, à l’équateur ou au pôle, il n’y a pas de déviation du fil à plomb. Notons que la discussion du fil à plomb est analogue à celle du pendule de Foucault, elle dépend de la latitude : la différence dans le cas du pendule de Foucault est qu’il est en mouvement.
Quelques ordres de grandeur :
G = 9,81 m x s-2
Accélération centrifuge (effet Eötvös) maximum égal à 1,7 x 10-3 m x s-2
Accélération de Coriolis 2 Ω v = 1,5 x 10-4 v, où v est la vitesse du mobile
NB : les deux accélérations, centrifuge et de Coriolis, sont des forces liées au repère terrestre, non galiléen. La force centrifuge est la composante " statique " de la force inertielle liée à la rotation terrestre, la force de Coriolis en est la composante " dynamique".
NB : les deux accélérations, centrifuge et de Coriolis, sont des forces liées au repère terrestre, non galiléen. La force centrifuge est la composante " statique " de la force inertielle liée à la rotation terrestre, la force de Coriolis en est la composante " dynamique".
Roland Eötvös va consacrer trente années de sa vie à l’étude de la force d’inertie terrestre pour un pendule qui n’est pas en mouvement ; certains appellent maintenant cette force " l’effet Eötvös ", comme " l’effet Coriolis " désigne l’autre force. Il utilise le " pendule de torsion "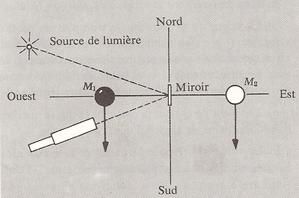 
Eötvös compare deux corps de même masse pesante mg (mg du corps 1 = mg du corps 2), et compare la force d’inertie sur ces deux corps, égal à mi Ω² R sinλ cosλ. Le dispositif utilisé est ingénieux : si cette force d’un côté est supérieure à l’autre (mi du corps 1 supérieure à mi du corps 2), on verra une torsion du fil mesurée par le déplacement d’un miroir. En fait Eötvös, prenant une masse de platine toujours identique d’un côté, et mettant d’autres corps de l’autre côté, n'observe pas de torsion, et mesure l’égalité de la masse inerte mi et de la masse pesante mg à 10-8 près.
Eötvös compare deux corps de même masse pesante mg (mg du corps 1 = mg du corps 2), et compare la force d’inertie sur ces deux corps, égal à mi Ω² R sinλ cosλ. Le dispositif utilisé est ingénieux : si cette force d’un côté est supérieure à l’autre (mi du corps 1 supérieure à mi du corps 2), on verra une torsion du fil mesurée par le déplacement d’un miroir. En fait Eötvös, prenant une masse de platine toujours identique d’un côté, et mettant d’autres corps de l’autre côté, n'observe pas de torsion, et mesure l’égalité de la masse inerte mi et de la masse pesante mg à 10-8 près. Partager cet article
Published by Alexandre Moatti
-
dans
D'autres quasi-indispensables physiques
commenter cet article …
commenter cet article …
