L'hydrogène est un élément dont on entend beaucoup parler, en ces temps d'énergie chère : pile à combustible (hydrogène), biomasse (hydrogène),... Intéressons-nous à cet élément chimique, le premier de la table des éléments.
Premier paradoxe : c'est l'élément le plus courant de l'Univers (75% d'hydrogène, 24% d'hélium, 1% d'autres éléments) - et pourtant on ne le découvre qu'en 1766 (le chimiste anglais Cavendish) - l'hélium, deuxième élément de la table, ne sera découvert que 100 ans plus tard ! alors que la plupart des éléments lourds étaient connus avant - par exemple l'uranium est isolé du minerai de pechblende en 1789, et apparaît comme une curiosité avant que Becquerel et les Curie ne s'y intéressent....
C'est l'élément le plus courant de l'Univers - et ne confondons pas composition chimique de l'Univers et composition chimique de notre atmosphère (80% d'azote et 20% d'oxygène...). Mais, même si l'hydrogène n'est pas un constituant de l'atmosphère, il est très abondant sur la Terre elle-même, puisqu'on le trouve dans l'eau H2O (70% de la surface de la planète), mais aussi dans les hydrocarbures (comme leur nom l'indique), les organismes vivants eux-mêmes principalement formés d'eau. A la différence de l'Univers, on ne le trouve sur Terre pratiquement jamais à l'état pur... toujours combiné à l'oxygène, ou au carbone. Second paradoxe.
Son nom lui-même est indissociablement lié à l'eau : le préfixe hydro- nous le rappelle (c'est Lavoisier qui baptise cet élément : générateur d'eau, hydrogène) ; en allemand H c'est... Wasserstoff.
A l'heure actuelle, H n'est pas utilisé pour des besoins énergétiques (une exception toutefois : l'hydrogène liquide comprimé à -250°C pour les moteurs de fusée, de type propergols) ... mais H est néanmoins largement utilisé, troisième paradoxe ! L'hydrogène est utilisé dans l'industrie chimique, pour la production d'ammoniac NH3 (engrais et produits ménagers notamment), dans d'autres industries, à hauteur de 50 millions de tonnes par an.
Comment produit-on cet hydrogène ? En utilisant le pétrole ou le gaz naturel (qu'on voudrait remplacer dans l'utilisation énergétique mondiale par... l'hydrogène, quatrième paradoxe !) : en effet 95% de H est produit par dissociation des molécules d'hydrocarbures, qui libèrent leur hydrogène. Les autres modes de production sont l'électrolyse de l'eau (procédé actuellement quatre fois plus coûteux) et... la biomasse : bois mort, paille,... leur gazéification est une source balbutiante de production d'hydrogène.
 Car cette petite molécule est fortement énergétique : 1 kg d'H libère 120 mégajoules, alors qu'1 kg d'essence en libère trois fois moins. Mais - il y a un mais - il est beaucoup moins dense, il faut le comprimer, pour libérer ces 120 mégajoules, il faut 13 litres d'H comprimés à 700 bars. En fait, cinquième paradoxe, ce n'est pas en tant que combustible lui-même mais pour produire de l'électricité que H est intéressant ! Une électricité portable, non reliée au réseau électrique, notamment pour toutes les utilisations de type « pile », donc les applications mobiles : téléphones, ordinateurs,... et moyens de transports (autobus, bientôt automobiles). C'est la PAC - pile à combustible - pour les véhicules électriques alimentés par une pile à hydrogène embarquée.
Car cette petite molécule est fortement énergétique : 1 kg d'H libère 120 mégajoules, alors qu'1 kg d'essence en libère trois fois moins. Mais - il y a un mais - il est beaucoup moins dense, il faut le comprimer, pour libérer ces 120 mégajoules, il faut 13 litres d'H comprimés à 700 bars. En fait, cinquième paradoxe, ce n'est pas en tant que combustible lui-même mais pour produire de l'électricité que H est intéressant ! Une électricité portable, non reliée au réseau électrique, notamment pour toutes les utilisations de type « pile », donc les applications mobiles : téléphones, ordinateurs,... et moyens de transports (autobus, bientôt automobiles). C'est la PAC - pile à combustible - pour les véhicules électriques alimentés par une pile à hydrogène embarquée.
L'enjeu de l'hydrogène dans le développement durable est donc multiple. D'abord arriver à produire H de manière économique et non productrice d'effet de serre (CO2) : électrolyse, biomasse... Et aussi accepter de modifier nos usages : le véhicule électrique à combustible, par exemple. Elément de base au coeur de la fusion des étoiles ou d'ITER, future source d'électricité pour nos usages mobiles, décidément cette petite molécule n'a pas fini de faire parler d'elle au XXI° siècle.
 (téléchargez l'intéressante brochure du CEA, cliquez sur l'image)
(téléchargez l'intéressante brochure du CEA, cliquez sur l'image)












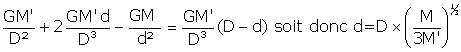 Pour le système Terre-Lune perturbé par le Soleil, on trouve une distance
Pour le système Terre-Lune perturbé par le Soleil, on trouve une distance 


 Etape 2 :
Etape 2 :

 Etape 5 :
Etape 5 :