24 juillet 2007
2
24
/07
/juillet
/2007
21:29
C’est le tricentenaire de la naissance du mathématicien suisse Euler (1707-1783) ; on connaît la célèbre relation d’Euler sur les polyèdres s + f - a = 2, où s est le nombre de sommets, a le nombre d’arêtes, f le nombre de faces.
Nous allons, avec cette relation, essayer de construire le ballon de football, en partant du principe qu’il est composé d’hexagones (au nombre de x) et de pentagones (au nombre de y), et en sachant que ce sont des bouts de cuir plats qu’on veut coudre pour en faire ce qui se rapproche le plus d’une sphère.
Il y a d’abord un peu de théorie derrière, liée à la nature des polyèdres réguliers : on sait qu’il n’existe qu’un nombre fini de tels polyèdres, du tétraèdre à l’icosaèdre, le plus grand, composé de 20 faces triangulaires. Il est important de comprendre qu’on ne peut pas construire de polyèdres réguliers avec des hexagones, ou tout polygone au-delà de l’hexa (heptagone, etc.) ; car, comme on le voit dans la figure ci-dessous, trois hexagones jointifs en leurs sommets pavent le plan, c’est à dire forment l’angle de 360°. Pour qu’on puisse le " refermer " en un solide de type polyèdre (on appelle cela aussi toîter la figure, en faire un toit), il faut que la somme des angles à chaque sommet soit strictement inférieure à 360°.
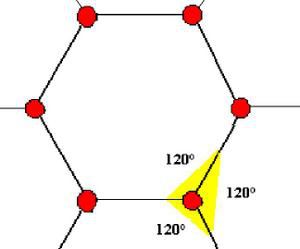
On ne peut donc pas prendre des polyèdres au-delà de l’hexagone pour construire le ballon ; on ne peut pas non plus prendre que des hexagones, car c’est le cas limite (chaque sommet donne 360°), qui ne marche pas. On se place donc juste en-dessous du cas limite, avec x pentagones et y hexagones.
Allons-y. On peut écrire les identités suivantes : f = x + y , a = ½ (5x + 6y), s = 1/3 (5x + 6y) (c’est assez facile, avec x hexagones et y pentagones, on a au total 5x + 6y côtés, et chaque côté est partagé entre deux faces du ballon ; même raisonnement pour les sommets). La relation d’Euler donne donc, en appliquant s – a + f = 2, le résultat x = 12 : y disparaît dans la résolution, mais on est sûr qu’il y a douze pentagones.
A partir de là, il y a plusieurs façons de raisonner :
Méthode 1 : Comme on sait que trois hexagones ne sont jamais jointifs (sinon on n’arriverait pas à replier, cf. théorie ci-dessus), à chaque sommet il y a au moins un pentagone, donc chaque sommet appartient à au moins un pentagone ; comme il y a 12 pentagones, il y a au plus 60 sommets dans le ballon. Pour que le ballon soit le plus rond possible, il faut qu’il y ait le maximum de sommets, donc s = 60 ; or s = 1/3 (5x + 6y), donc y = 20.
Méthode 2 : Comme on ne peut fermer le solide avec trois hexagones en un point, en chaque point il y a soit : a/ deux hexagones et un pentagone (120 + 120 + 108 qu’on peut refermer) ; b/ un hexagone et deux pentagones (120 + 108 + 108) ; c/ trois pentagones (108 + 108 + 108). Le cas optimal dans le sous-optimal (le plus proche d’une sphère) est celui où on est le plus proche de 360, donc c’est le cas a/. Dans ce cas, chaque sommet appartient à un et un seul pentagone, il y a donc bien 60 sommets exactement, donc on déduit comme ci-dessus y = 20.
A signaler que le cas c/ ci-dessus (que des pentagones, disparition des hexagones) conduit au solide à 12 pentagones, c’est le dodécaèdre à 12 faces et 20 sommets : voir ci-contre, cela ressemble à un ballon de foot mais n’en est pas un. Je ne sais pas à quel solide correspond le cas b/, s’il correspond à quelque chose.
Le cas a/ est le ballon de foot (douze pentagones et vingt hexagones), et on peut remarquer que c’est " l’icosaèdre tronqué ", c’est à dire le plus grand solide auquel on a rogné les pointes (on tronque chaque triangle au tiers de la pointe) pour le rapprocher d’une sphère, chacune des douze pointes devenant un pentagone, et chacune des vingt faces triangulaires devenant un hexagone :
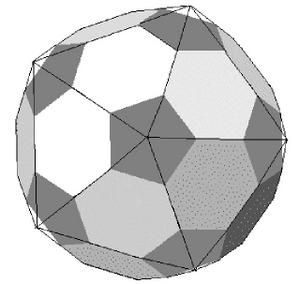
Cà y est, vous n'avez plus qu'à coudre le patron composé de 12 pentagones et 20 hexagones: a = 90 donc 90 coutures:
(image S. Mehl) Pour aller beaucoup plus loin (la théorie complète) (PDF)
(ajout février 2010) voir aussi le billet simplifié que j'ai fait dans le site Futura-Sciences
(ajout février 2010) voir aussi le billet simplifié que j'ai fait dans le site Futura-Sciences
Partager cet article
Published by Alexandre Moatti
-
dans
D'autres quasi-indispensables mathématiques
commenter cet article …
commenter cet article …
