 La lecture du livre de Marcel Berger (Géométrie vivante, ou l'échelle de Jacob, Cassini 2009 – livre ardu mais passionnant – il porte bien son titre, c'est vivant) m'a ouvert les yeux sur la géométrie du tore – un tore c'est un beignet ou une bouée ou un pneu. Il existe quatre familles de cercles à la surface d'un tore : les méridiens (on coupe des tranches de bouée comme un saucisson), les parallèles (on coupe par un plan parallèle à l'eau, pour une bouée), et les cercles de Villarceau – mais où sont ces cercles ? Berger nous dit qu'il a été abasourdi, à l'âge de 16 ans, de découvrir l'existence de ces cercles, et qu'il a même coupé un anneau en bois afin de les voir….. Moi-même, quelques années après mes 16 ans, je suis aussi abasourdi – mais où sont ces cercles ?
La lecture du livre de Marcel Berger (Géométrie vivante, ou l'échelle de Jacob, Cassini 2009 – livre ardu mais passionnant – il porte bien son titre, c'est vivant) m'a ouvert les yeux sur la géométrie du tore – un tore c'est un beignet ou une bouée ou un pneu. Il existe quatre familles de cercles à la surface d'un tore : les méridiens (on coupe des tranches de bouée comme un saucisson), les parallèles (on coupe par un plan parallèle à l'eau, pour une bouée), et les cercles de Villarceau – mais où sont ces cercles ? Berger nous dit qu'il a été abasourdi, à l'âge de 16 ans, de découvrir l'existence de ces cercles, et qu'il a même coupé un anneau en bois afin de les voir….. Moi-même, quelques années après mes 16 ans, je suis aussi abasourdi – mais où sont ces cercles ?
 (figure ci-dessus, extraite du livre de Berger – assez sympa qu'il y ait certaines figures à la main – çà désacralise) Ces cercles correspondant en fait à la coupe par un plan bitangent : c'est-à-dire un plan horizontal tangent en haut d'un côté de la bouée, passant par le centre, et tangent en bas de l'autre côté de la bouée. Berger nous dit en légende : "Le lecteur pourra se convaincre à sa façon de la réalité des cercles de Villarceau"
(figure ci-dessus, extraite du livre de Berger – assez sympa qu'il y ait certaines figures à la main – çà désacralise) Ces cercles correspondant en fait à la coupe par un plan bitangent : c'est-à-dire un plan horizontal tangent en haut d'un côté de la bouée, passant par le centre, et tangent en bas de l'autre côté de la bouée. Berger nous dit en légende : "Le lecteur pourra se convaincre à sa façon de la réalité des cercles de Villarceau"
J'aime bien ce genre de légendes : çà marche, car finalement le lecteur se prend au jeu. La page Wikipedia est certes intéressante; je ne suis pas sûr qu'Yvon Villarceau aurait décrit « ses » cercles (qui, au passage, étaient connus bien avant lui !) ainsi, avec des équations cartésiennes ou avec la fibration de Hopf ! le seul problème c'est que je ne comprends pas l'animation sur la page... Alors, pour me « convaincre », j'ai essayé une autre construction.

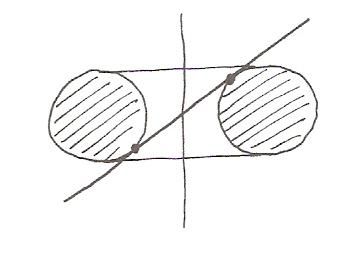
Je prends un plan vertical qui coupe le tore, et je vais le faire pivoter à 90° en un plan horizontal qui coupe le tore, en regardant les positions intermédiaires. Donc au départ (à gauche ci-dessus), plan vertical, deux tranches de saucisson (méridiens). A l'arrivée (à droite ci-dessus), deux cercles concentriques (parallèles). Et entre, que se passe-t-il ?
1) On part de la gauche, on incline notre plan, les deux points marqués à droite (ainsi que les symétriques à gauche, non marqués) restent les mêmes ; la surface de coupe du plan par le tore devient une espèce de haricot – je n'en suis pas sûr mais je pense que c'est cela. Pour s'en "convaincre", on coupe un bout de cylindre par un plan (ellipse), on tord en tore le bout de cylindre, l'ellipse se tord.
2) On part de la droite, on incline notre plan, les deux points marqués à droite (ainsi que les symétriques à gauche, non marqués) restent les mêmes ; le cercle extérieur s'aplatit en ellipse, le cercle intérieur s'agrandit en ellipse – on peut l'illustrer ainsi : les deux points marqués sur figure ci-dessus restent fixes quand on fait tourner notre plan, et les autres points, à 90°, donnent la figure ci-dessus quand notre plan part de l'horizontale (ci-dessus à droite); la distance au point extérieur diminue de OA en OA', celle du point intérieur OB augmente.

Mais alors, encore une fois, où sont-ils ces fameux cercles de Villarceau ? eh bien, on va les trouver à la place du point d'interrogation ci-dessus, comme une animation des figures voisines, par la droite ou par la gauche :

A gauche, les deux figures vont peu à peu se rapprocher pour former deux cercles, le périmètre externe d'une des figures (vert à gauche) venant relier le périmètre interne de l'autre (vert au milieu) ; idem à droite; idem pour les figures rouges ; venant de la droite ou de la gauche, cela forme au point de bitangence la figure du milieu, celle des deux cercles de Villarceau, et dans l'espace les voici (image Wikipedia) :

Voici donc comment deux cercles séparés, les méridiens (à gauche, première figure ci-dessus sous le trait), se transforment en deux cercles concentriques, les parallèles (à droite même figure), en passant par deux cercles entrelacés style anneaux olympiques, les cercles de Villarceau.
(ajoût d'avril 2010) voir récent article de Marcel Berger sur les cercles de Villarceau dans BibNum
commenter cet article …








